그래프(Graph)
- 그래프는 tree의 상위개념으로
- 그래프(Graph)란 사물을 정점(vertax)와 간선(edge)으로 이루어져있다.
- 그래프는 두 가지 방식으로 구현할 수 있다.
- 인접 행렬(adjacency matrix): 2차원 배열을 사용하는 방식
- 인접 리스트(adjacency list): 연결 리스트를 이용하는 방식
인접 행렬(Adjacency Matrix)
- 인접행렬(adjacency matrix)에서는 그래프를 2차원 배열로 표현한다.
- 가중치가 0인 경우와 대비하기 위해 ∞로 표시하기도 한다.

인접행렬 - 무방향 무가중치 그래프
- 모든 간선이 방향성을 가지지 않는 그래프를 부방향 그래프라고 한다.
- 모든 간선에 가중치가 없는 그래프를 무가중치 그래프라고 한다.
- 무방향 비가중치 그래프가 주어졌을 때 연결되어 있는 상황을 인접 행렬로 출력할 수 있다.
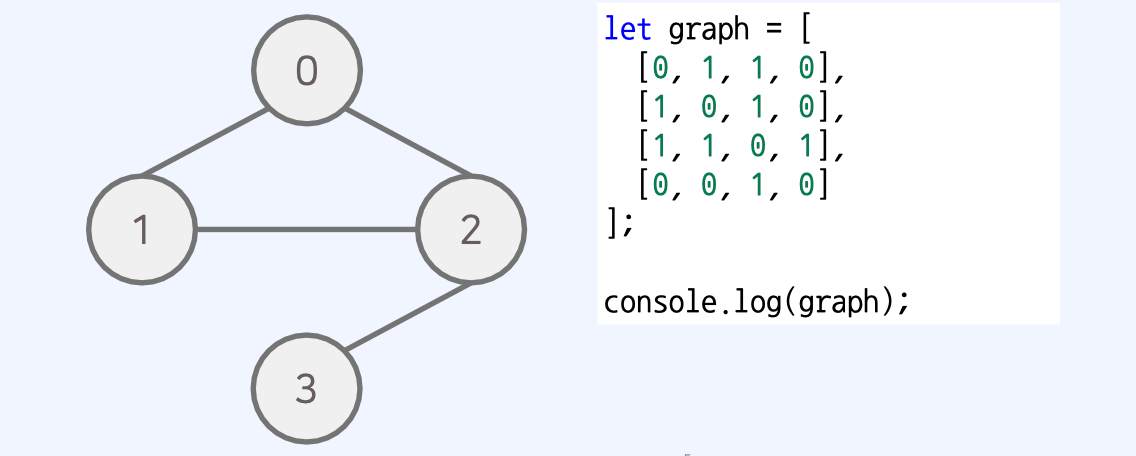
인접행렬 - 방향 가중치 그래프
- 모든 간선이 방향을 가지는 그래프를 방향 그래프라고 한다.
- 모든 간선에 가중치가 있는 그래프를 가중치 그래프라고 한다.
- 방향 가중치 그래프가 주어졌을 때 연결되어 있는 상황을 인접 행렬로 출력할 수 있다.
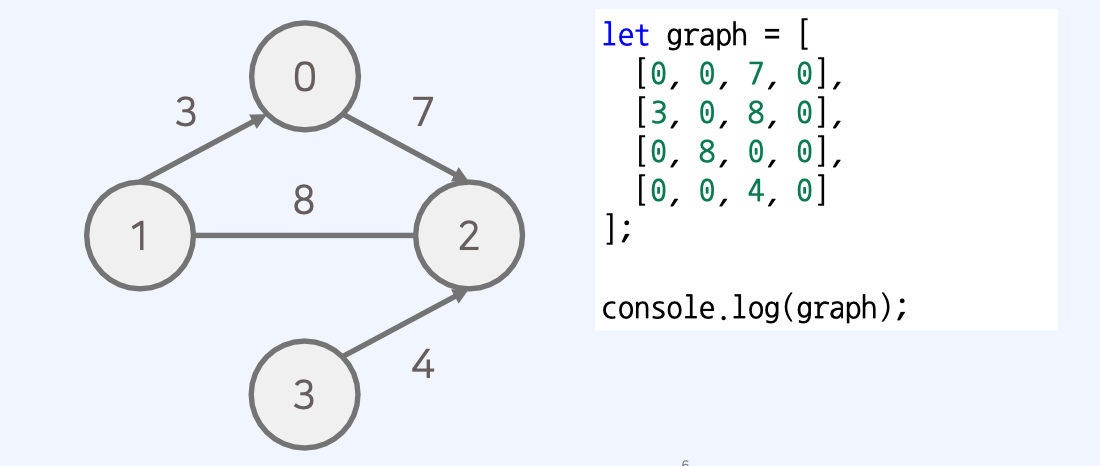
인접 리스트(Adjacency List)
- 인접 리스트(adjacency list)에서는 그래프를 리스트로 표현한다.

인접행렬 - 무방향 무가중치 그래프
- 모든 간선이 방향을 가지지 않는 그래프를 무방향 그래프라고 한다.
- 모든 간선에 가중치가 없는 그래프를 무가중치 그래프라고 한다.
- 무방향 비가중치 그래프가 주어졌을 때 연결되어 있는 상황을 인접 리스트로 출력할 수 있다.

인접행렬 - 방향 가중치 그래프
- 모든 간선이 방향을 가지는 그래프를 방향 그래프라고 한다.
- 모든 간선에 가중치가 있는 그래프를 가중치 그래프라고 한다.
- 방향 가중치 그래프가 주어졌을 때 연결되어 있는 상황을 인접 리스트로 출력할 수 있다.

그래프의 시간 복잡도
- 인접 행렬: 모든 정점들의 연결 여부를 저장해 𝑂(𝑉^2) 의공간을요구한다.
- 공간 효율성이 떨어지지만, 두 노드의 연결 여부를 𝑂(1)에 확인할 수 있다.
- 인접 리스트: 연결된 간선의 정보만을 저장하여 𝑂(𝑉+𝐸)의 공간을 요구한다.
- 공간 효율성이 우수하지만, 두 노드의 연결 여부를 확인하기 위해 𝑂(𝑉)의 시간이 필요하다.
| 필요한 메모리 | 연결 여부 확인 | |
| 인접 행렬 | 𝑂(𝑉^2) | 𝑂(1) |
| 인접 리스트 | 𝑂(𝑉+𝐸) | 𝑂(𝑉) |
인접 행렬 vs 인접 리스트
- 최단 경로 알고리즘을 구현할 때에는, 각각 근처의 노드와 연결되어 있는 경우가 많으므로 간선개수가 적어 인접 리스트가 유리하다.
'자료구조 & 알고리즘 > 자료구조' 카테고리의 다른 글
| [자료구조]_트리(Tree)와 우선순위 큐(Priority Queue) (0) | 2023.03.29 |
|---|---|
| [자료구조]_큐(Queue) (0) | 2023.03.29 |
| [자료구조]_스택(Stack) (0) | 2023.03.11 |
